A. Gerak Melingkar Beraturan.
Benda
dikatakan bergerak melingkar beraturan jika lintasannya berupa
lingkaran dengan kelajuan tetap,.ingat bukan kecepatan tetap. Hal ini
dapat dijelaskan melalui gambar berikut,
Pada
gambar di atas kelajuan materi dititik A, B, C dan D bernilai sama atau
tetap. Namun arahnya di setiap titik tersebut berbeda. Hal inilah yang
membedakan antara laju dan kecepatan gerak benda melingkar. Kecepatan di
A dengan arah ke atas, kecepatan di titik B arah ke kiri, kecepatan di
titik C arah ke bawah dan kecepatan di D arah ke kanan.
Beberapa besaran pada gerak melingkar beraturan
1. Periode dan Frekuensi
Periode (T) putaran sebuah benda didefinisikan sebagai waktu yang diperlukan untuk satu kali putaran. Jika untuk menempuh satu kali putaran diperlukan waktu 5 sekon maka boleh dikatakan periode putaran benda (T) tersebut adalah 5 sekon. Jika untuk menempuh n putaran diperlukan waktu selama t sekon, maka periode benda dapat dinyatakan dalam persamaan sebagai berikut :
Dimana :
T = periode (sekon)
t = waktu selama putaran (sekon)
n = banyaknya putaran
Frekuensi (f) adalah banyaknya putaran persatuan waktu. Jika sebuah roda berputar pada porosnya 10 kali putaran selama 5 sekon maka frekuensi perputaran roda tersebut sebesar 2 Hz. Jika untuk melakukan n putaran memerlukan waktu t sekon maka frekuensi dapat dinyatakan dalam persamaan :
Hubungan antara periode (T) dan frekuensi dinyatakan dalam persamaan berikut :
atau :
Contoh soal : Periode (T) putaran sebuah benda didefinisikan sebagai waktu yang diperlukan untuk satu kali putaran. Jika untuk menempuh satu kali putaran diperlukan waktu 5 sekon maka boleh dikatakan periode putaran benda (T) tersebut adalah 5 sekon. Jika untuk menempuh n putaran diperlukan waktu selama t sekon, maka periode benda dapat dinyatakan dalam persamaan sebagai berikut :
Dimana :
T = periode (sekon)
t = waktu selama putaran (sekon)
n = banyaknya putaran
Frekuensi (f) adalah banyaknya putaran persatuan waktu. Jika sebuah roda berputar pada porosnya 10 kali putaran selama 5 sekon maka frekuensi perputaran roda tersebut sebesar 2 Hz. Jika untuk melakukan n putaran memerlukan waktu t sekon maka frekuensi dapat dinyatakan dalam persamaan :
Hubungan antara periode (T) dan frekuensi dinyatakan dalam persamaan berikut :
atau :
Sebuah materi melakukan gerak melingkar selama 5 menit. Jika dalam waktu tersebut , materi telah melakukan 600 putaran maka frekuensi dan periode putaran materi tersebut adalah....
Solusi :
Materi telah melakukan 600 putaran (n) selama 5 menit = 5 x 60 sekon = 300 sekon (t), maka :
a. f = n/t = 600/300 = 2 Hz
b. T = t/n = 300/600 = 0,5 sekon
atau untuk mencari T = 1/f, sehingga T = 1/2 sekon.
2. Kecepatan sudut dan kecepatan linier
Kecepatan sudut didefinisikan sebagai besar sudut yang ditempuh tiap satu satuan waktu. Dalam gerak melingkar beraturan, kecepatan sudut atau kecepatan anguler untuk selang waktu yang sama selalu konstan. Untuk partikel yang melakukan gerak satu kali putaran, berarti sudut yang ditempuh adalah 360 derajat atau 2 pi dan waktu yang diperlukan untuk satu kali putaran disebut satu periode (T). Maka kecepatan sudut dapat dinyatakan dalam persamaan berikut :
Hubungan antara kecepatan sudut dengan kecepatan linier dapat dinyatakan dalam persamaan berikut :
Karena
Maka :







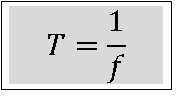





.gif)
.gif)
.gif)
.gif)
.gif)
.gif)
.gif)
.gif)
.gif)
.gif)










